TEMA 3: Teorema de Pitágoras

Actividades a desarrollar

1. Escribe la explicitación del Teorema de Pitágoras

   • Redacta una explicación clara y completa del teorema, incluyendo la fórmula $a^2 + b^2 = c^2$.

2. Dibuja un triángulo con los catetos y la hipotenusa

   • Traza un triángulo rectángulo.
   • Etiqueta los catetos ($a$ y $b$) y la hipotenusa ($c$).

3. Escribe los ejercicios de explicación del video y resuelve los que aparecen al final

   • Toma notas de los ejercicios explicados en el video.
   • Reproduce los pasos de cada solución por escrito, asegurándote de entender cada procedimiento.
   • Resuelve los problemas propuestos al final del video, detallando los cálculos y justificando tus respuestas.

4. Contesta el problemario que viene al final

• Lee cuidadosamente cada problema.
• Aplica el Teorema de Pitágoras para resolverlos, explicando cada paso de manera ordenada y lógica.
• Comprueba tus respuestas para asegurarte de que sean correctas.

Nota: Todo lo necesario para las actividades están incluidas en esta entrada de blog que te he preparado.

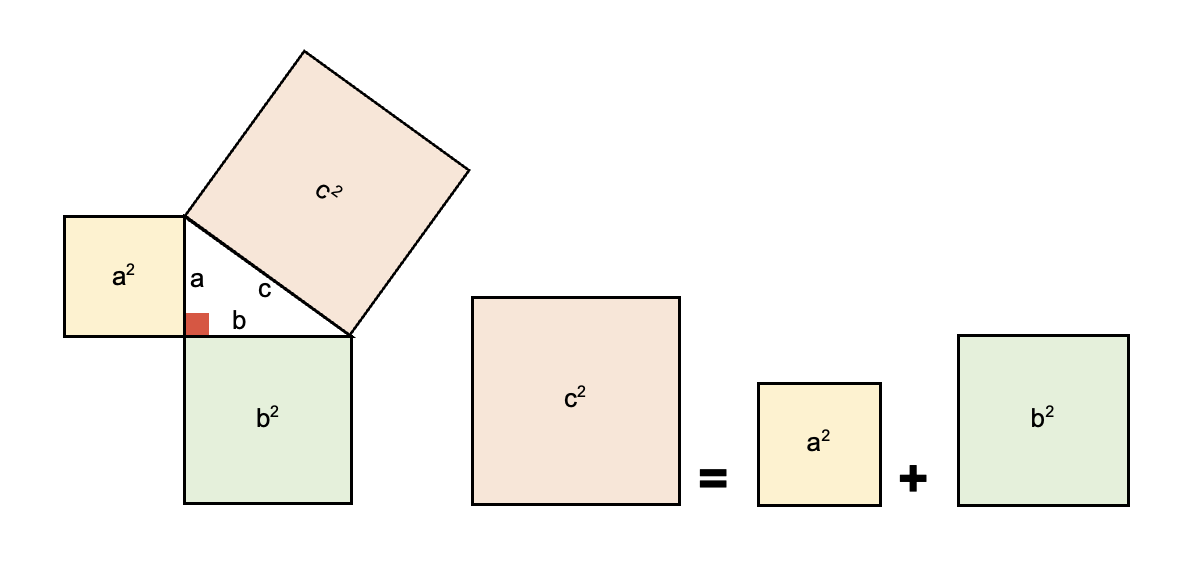
El Teorema de Pitágoras es una de las herramientas más poderosas y versátiles en el aprendizaje de las matemáticas. Este principio, atribuido al matemático griego Pitágoras, establece que:

"En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos".

En términos matemáticos:

$$a^2 + b^2 = c^2$$

donde $a$ y $b$ son los catetos, y $c$ es la hipotenusa, el lado opuesto al ángulo recto.

¿Por qué es relevante?

El Teorema de Pitágoras no solo es un concepto teórico, sino que encuentra aplicaciones prácticas en la resolución de problemas cotidianos, como:

• Cálculo de distancias: Determinar la longitud más corta entre dos puntos.
• Diseño y construcción: Medir dimensiones exactas en estructuras como techos o escaleras.
• Navegación: Estimar trayectorias en mapas y coordenadas.

Explicitación del Teorema

El Teorema de Pitágoras se aplica exclusivamente a triángulos rectángulos, lo que significa que uno de sus ángulos es de $9{\mathrm{0°}}^{}$. Para usarlo correctamente, es importante identificar:

1. Los catetos: Los lados que forman el ángulo recto.
2. La hipotenusa: El lado más largo, que se encuentra opuesto al ángulo recto.

Una vez identificados, basta con sustituir las longitudes conocidas en la fórmula $a^2 + b^2 = c^2$ y resolver para encontrar la incógnita.

A continuación, el siguiente video contiene la explicación detallada del tema.

Resolviendo problemas con el Teorema de Pitágoras

Veamos un ejemplo práctico:

Problema: Un bombero necesita una escalera para alcanzar una ventana que está a 6 metros de altura y situada 8 metros de distancia horizontal desde el pie de la escalera. ¿Qué longitud debe tener la escalera?

Solución:

1. Identifica las partes del triángulo:

   • $a = 6$ m (altura de la ventana).
   • $b = 8$ m (distancia horizontal).
   • $c = ?$ m (longitud de la escalera).

2. Aplica el Teorema de Pitágoras:

   $$c^2 = a^2 + b^2$$
   

   Sustituimos los valores:

   $$c^2 = 6^2 + 8^2$$
   $$c^2 = 36 + 64$$
   $$c^2 = 100$$
   

3. Resuelve:

   $$c = \sqrt{100} = 10$$
   

Por lo tanto, la escalera debe medir 10 metros.

Resolviendo problemas con el Teorema de Pitágoras: Caso con Resta

El Teorema de Pitágoras también es útil cuando ya conocemos la hipotenusa y uno de los catetos, y necesitamos encontrar el otro cateto. En estos casos, reorganizamos la fórmula para resolver mediante resta:

$$a^2 = c^2 - b^2 \quad \text{o} \quad b^2 = c^2 - a^2$$

Problema:

Una persona camina desde un punto A hasta un punto B en línea recta, recorriendo 13 metros. Luego se desvía en un ángulo recto y camina otros 5 metros hacia un punto C. ¿Qué distancia hay entre los puntos A y C?

Solución:

1. Identifica las partes del triángulo:

   • Hipotenusa ($c$) = 13 m (distancia total desde A hasta B).
   • Un cateto ($b$) = 5 m (distancia desde B hasta C).
   • Cateto desconocido ($a$) = ? (distancia desde A hasta C).

2. Reorganiza el Teorema de Pitágoras:
   Para encontrar un cateto, usamos:

   $$a^2 = c^2 - b^2$$
   

3. Sustituye los valores conocidos:

   $$a^2 = 13^2 - 5^2$$
   $$a^2 = 169 - 25$$
   $$a^2 = 144$$
   

4. Resuelve:

   $$a = \sqrt{144} = 12$$
   

Por lo tanto, la distancia entre los puntos A y C es 12 metros.

Problemario del Teorema de Pitágoras

Descarga el problemario aquí:

Problemario del Teorema de Pitágoras (PDF)